前回は、関数\( y=a x^2\)について学習しました。ここでは、そのグラフについて学習していきます。
関数\( y=x^2\)のグラフ
まず、手始めに関数\( y=x^2\)のグラフを描いていきたいと思います。そのために、関数\( y=x^2\)について、\( x\)と\( y\)の値の組をそれぞれ表に書いていきます。
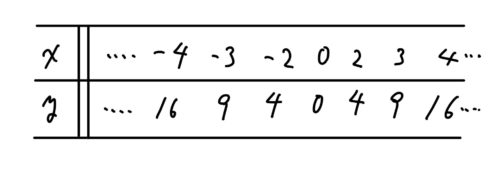
次にこの表の値を図に書き入れていきます。この表を見ると今まで学習したものとの違いを感じてもらえると思います。
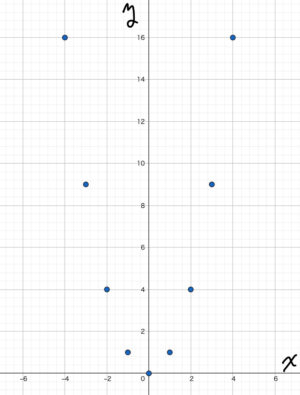
さらに\( x\)と\( y\)の値の組を増やして調べていきます。

図に書き入れていきます。
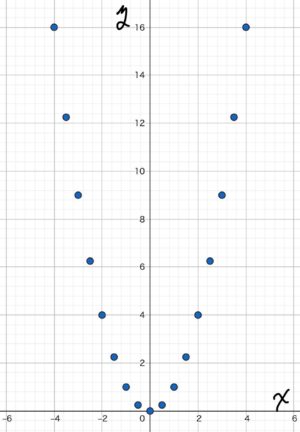
もっと調べる点を増やすと下のようになります。
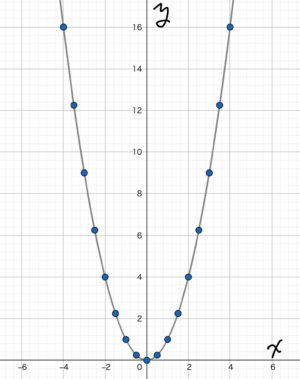
まとめ

関数\( y=ax^2\)のグラフ
次にもっと一般の場合を考えていきます。
a>0のとき
まず、\( a\)の値が正のときの場合を考えていこうと思います。
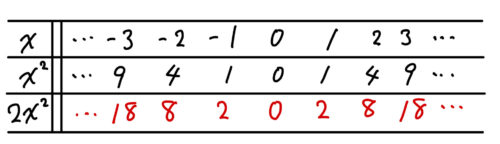
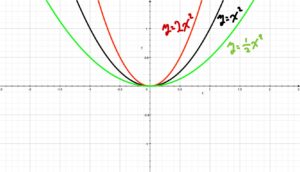
\(y=2x^2 \)のグラフ
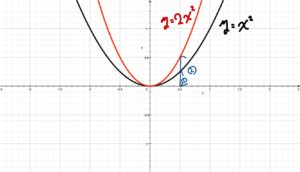
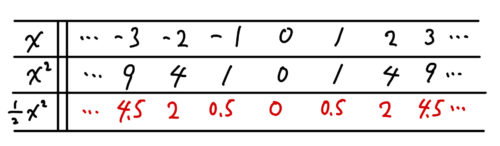
\( \displaystyle y=\frac{1}{2}x^2 \)のグラフ
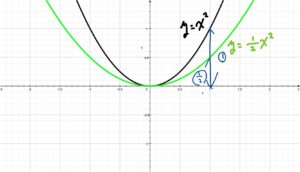
\( a\)の値が変化したときグラフの開き方はどうなるか?
a<0のとき
\( y=-x^2\)
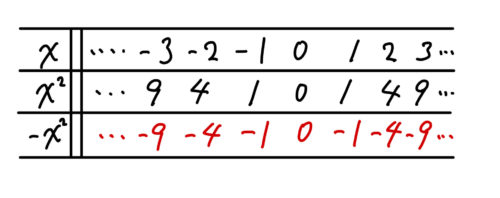
この表を見るとある数\( x\)に対応するする\( -x^2\)の値は、同じ\( x\)の値に対応する\( x ^{2} \)の値と絶対値が等しく符号が反対になっています。(例えば、\( x=2\)のとき\( x ^{2} =4,- x ^{2} =-4\) )
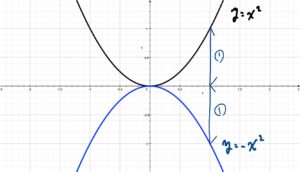
したがって、関数\( y=- x ^{2} \)のグラフは関数\( y=x ^{2} \)のグラフの各点と、\( x\)軸について対称な点の集まりであることがわかります。
つまり、2つの関数\( y=x ^{2} \)、\(y=x ^{2} \)のグラフは、\( x\)軸について対称になっています。
\( a\)の値が変化したときグラフの開き方はどうなるか?
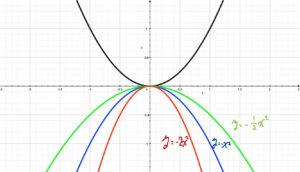
まとめ
[1]原点を通り、\( y\)軸について対称な曲線である。
[2]\( a>0\)のとき、上に開き、\( a<0\)のとき、下に開いている。
[3]\( a\)の絶対値が大きいほど、グラフの開き具合は小さくなる。
[4]2つの関数\( y= ax ^{2} \)、\( y= -ax ^{2} \)のグラフは\( x\)軸について対称である。
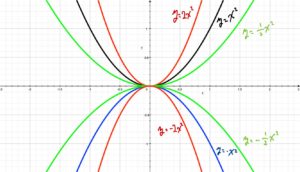
放物線の対称軸を、その放物線の軸といい、放物線と軸との交点を、その放物線の頂点と言います。
関数\( y=a x ^{2} \)のグラフを放物線\( y=a x ^{2} \)といい、\( y=ax ^{2} \)を放物線の式と言います。


コメント