【数II】不等式の証明【式と証明（第7回）】

実数の大小関係

実数の2乗と不等式

正の数の大小と平方の大小

絶対値と不等式

相加平均と相乗平均

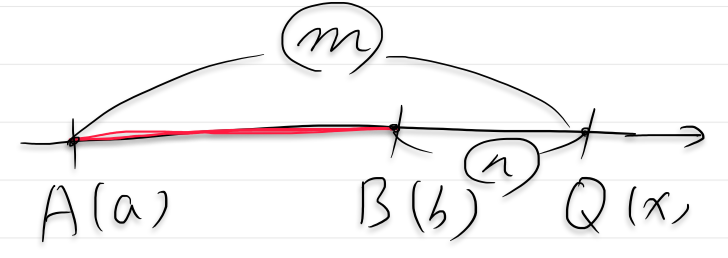
2数の平均を取るというと、”2数を足して2で割る”というのが一般的だと思いますが、数学では”2数で掛けて平方根をとる”という平均を考えることもあります。

一般的に、正の実数\(a,\ b \)に対して、\(\displaystyle \frac{a + b}{2} \)を\(a \)と\(b \)の相加平均、\( \displaystyle \sqrt{ab}\)を\( a\)と\( b\)の相乗平均といいます。

相加平均と相乗平均の間には、次のような不等式が成り立ちます。

証明）
\begin{align*} \frac{a + b}{2}-\sqrt{ab} &=\frac{1}{2}(a – 2 \sqrt{ab} – b )\\ &= \frac{1}{2}\left\{   (\sqrt{a} )  ^{2}  – 2  \sqrt{a}\sqrt{b}  + (\sqrt{b}) ^{2}  \right\}  \\ &=   \frac{1}{2}(\sqrt{a} – \sqrt{b}) ^{2}  \\ & ≧ 0 \end{align*} 
したがって、\begin{align*} \frac{a + b}{2} &≧ \sqrt{ab}\end{align*}
また、この不等式において等号が成立するのは\begin{align*} (\sqrt{a} – \sqrt{b})^{2}  &=0 \end{align*}すなわち、\begin{align*} \sqrt{a}- \sqrt{b}&=0 \end{align*}つまり、\begin{align*} a&=b \end{align*}のときである。