面積が1㎠である正方形の1辺の長さは1㎝です。また、面積が4㎠である正方形の1辺の長さは2㎝になります(実際、\( 2 \times 2=4\) )。では、面積が3㎠である正方形の1辺の長さは何㎝になるでしょうか?1㎝より大きく2㎝より小さくなることは分かると思いますが………。ここでは、2乗して\( a\)になる数について学習します。
平方根
面積が2㎠である正方形の1辺の長さは、
2乗して2になる数
になるはずである。
2乗して\( a\)になる数を、\(a \)の平方根といいます。
\( 3 ^{2}=92\)、\( (-3) ^{2}=9 \)であるので、2乗して9になる数は、正の数3と負の数−3の2つあります。したがって、3と−3は9の平方根になります。
2乗して\( a\ \)になる数を、\(a\ \)の平方根といいます。
次の数の平方根を求めなさい。
(1) 9 (2) 4 (3) 25 (4) 1
次の数の平方根を求めなさい。
(1) \(\displaystyle \frac{9}{25} \) (2) \(\displaystyle \frac{4}{49} \) (3) \(\displaystyle \frac{16}{81} \) (4) 0.09
どのような数を2乗しても負の数にはならないので、負の数の平方根はない。また、2乗して0になる数は0のみである。したがって、0の平方根は0のみである。
[1]正の数の平方根は2つあります。
この2つの数は絶対値が等しく、符号が異なります。(−△と+△)
[2]0の平方根は0だけです
根号
面積が2㎠である正方形の1辺の長さは、2乗して2になる数になるはずである。その数は、正の数と負の数の2つがありますが、正方形の辺なので正の数の方が求めたい長さになっている。
一辺を\( x\ \)㎝とします。このとき\( x ^{2} =2\)となっている。
では、\( x\ \)の値は具体的にいくつなのでしょうか?
\( x=1.414213562\cdots \cdots\)
のようにどこまでも続く小数であることが知られています。
このままだと計算しにくいので新しい記号を導入したいと思います。
\( x ^{2} =2\)を満たす正の数\( x\)を、記号\( \sqrt{ }\)を使って\( \sqrt{2}\)と書き、”ルート2”と読みます。
一般に、\( a\)を正の数とするとき、\( a\)の2つの平方根のうち
正の方を\( \sqrt{a}\) 、負の方を\(-\sqrt{a} \)
と書きます。
記号\( \sqrt{ }\)を根号(こんごう)といいます。
0の平方根は0だけであるので、\( \sqrt{0}=0\)とする。
\( a\ \)を正の数とする、\( a\ \)の平方根のうち
正の方を\( \sqrt{a}\ \)、負の方を\( -\sqrt{a}\ \)と書く。
記号\( \sqrt{\ \ }\ \)を根号といいます。
0の平方根は0だけであるので\( \sqrt{0}=0\ \)とします。
3の平方根のうち
正の方は\(\sqrt{3} \)、負の方は\(-\sqrt{3} \)
である。
(\sqrt{a} )と(-\sqrt{a} )をまとめて\(\pm\sqrt{a} \)と書くことがあります。これを、”プラス マイナス ルート a”と読みます。この記号を使うと3の平方根は\( \pm 3\)と書くことができます。
次の数の平方根を根号\( \sqrt{ }\)を使って表しなさい。
(1) 5 (2)13 (3) \(\displaystyle \frac{3}{5} \) (4) 0.3
近似値
面積が2㎠である正方形の1辺の長さは、およそ1.4㎝になります。1.4は真の値\( \sqrt{2}\)とは異なるが物差しで長さを求めても、これ以上正確な値を求めることは困難である。
真の値に近い値のことを近似値(きんじち)といいます。1.4、1.41、1.414などは\(\sqrt{2} \)の近似値である。円周率として使っている3.14も近似値である。
計算機の\( \sqrt{ }\)キーを使って、\( \sqrt{3}\)の近似値を求めましょう。
\( (\sqrt{a}) ^{2} \)と\( (-\sqrt{a}) ^{2} \)の値
2乗して\( a\)になる数が\( a\)の平方根であるので、\( a\)とその平方根\(\sqrt{a},\ -\sqrt{a}\)の関係は、次のようになります。
\( (\sqrt{a}) ^{2} =a\)
\( (-\sqrt{a}) ^{2} =a \)
\( (\sqrt{3}) ^{2} =3\) 、\(-\sqrt{3}) ^{2} =3 \)
次の値を求めなさい。
(1) \( \left(\sqrt{5}\right)^{2} \) (2) \( \left(-\sqrt{7}\right)^{2} \) (3) \( -\left(\sqrt{6}\right)^{2} \) (4) \(- \left(-\sqrt{2}\right)^{2} \)
根号を使わずに表すことができる数
一般に、\( a\)が正の数であるとき、\(\sqrt{a ^{2} }=a \)となります。
次の数を根号を使わずに表しなさい。
(1) \( \sqrt{4} \) (2) \( -\sqrt{25} \) (3) \( \displaystyle \sqrt{\frac{4}{25} } \)
(4) \(-\sqrt{0.09} \) (5) \(\sqrt{121} \) (6) \( \sqrt{(-13)^{2} }\)
次の(1)〜(4)には誤りがあります。下線部をなおして、正しい文にしなさい。
(1) \( \sqrt{36} \)は\( \pm 6\)である。 (2) 16の平方根は4である。
(3) \( \sqrt{(-5)^{2} } =-5\)である。 (4) \(\sqrt{0.9} \)と0.3は等しい。
平方根の大小
平方根の大小を比較する方法を学習していきます。
\( a\)が正の数であるとき、\(\sqrt{a} \)は”面積が\( a\)である正方形の1辺の長さ”と考えることができます。
\( a,\ b\)は正の数で、\( a<b\)とする。
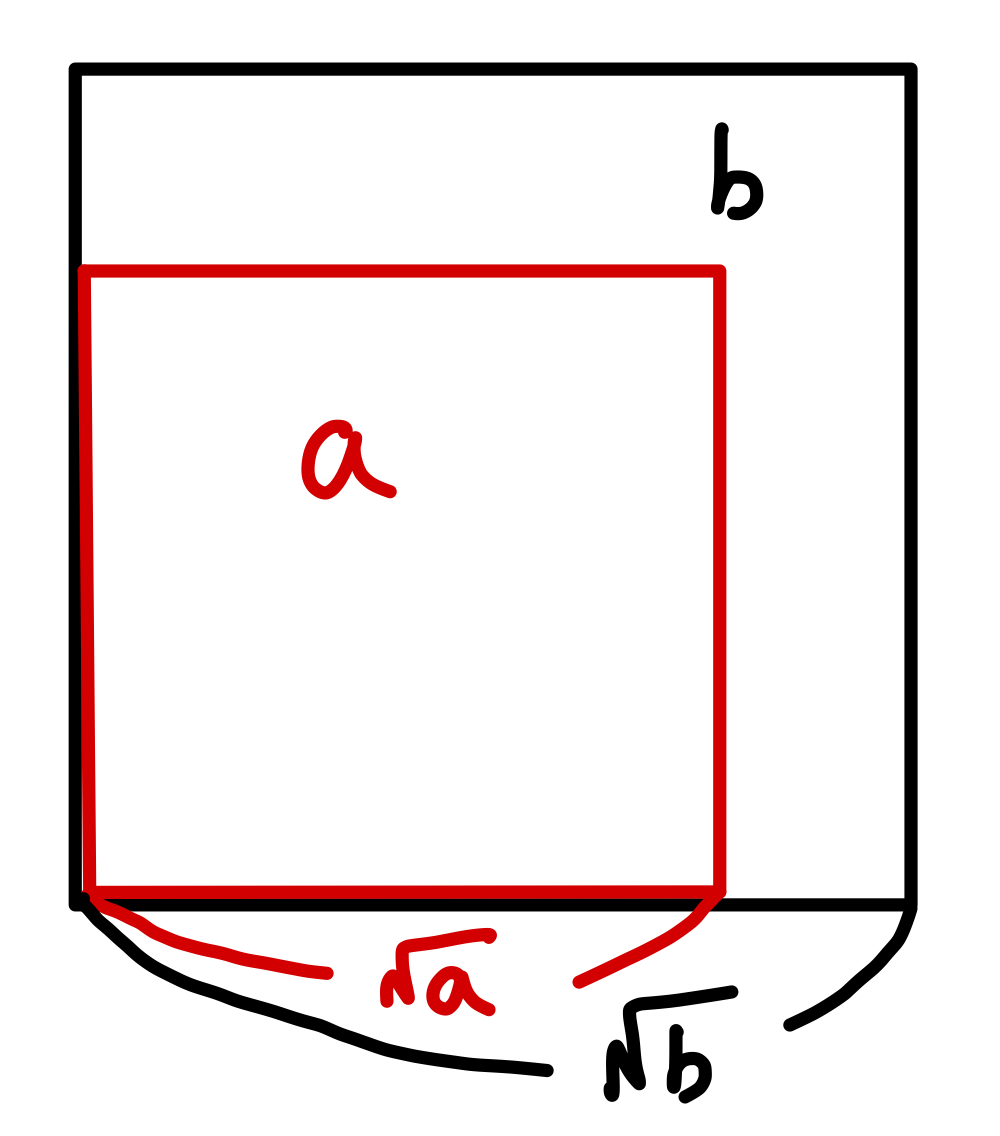
面積が\( a,\ b\)である2つの正方形を下の図のように重ねて、それぞれの1辺の長さを考えると、次のことがわかります。
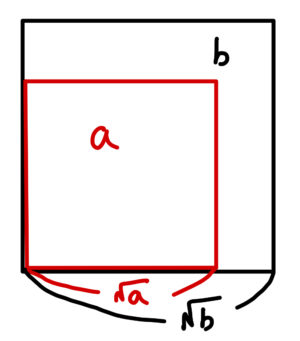
\( a\ \)、\( b\ \)が正の数のとき\[ a<b \ \mbox{ならば}\ \sqrt{a} <\sqrt{b} \]
\( 2<3\)であるので
\( \sqrt{2}<\sqrt{3}\)
である
3と\(\sqrt{8}\)の大小を不等号で表しましょう。
\( 3 ^{2} =9,\ \left(\sqrt{8}\right) ^{2} =8\)
で\( 8<9\)であるので
\( \sqrt{8}<\sqrt{9}\)
\( \sqrt{8}<3\)
である
次の2つの数の大小を、不等号を使って表しなさい。
(1) \( \sqrt{3},\ \sqrt{5}\) (2) \( \sqrt{15},\ 4\)
(3) \( -\sqrt{5},\ -\sqrt{6}\) (4) \( -3 ,\ -\sqrt{8} \)
次の2つの数の大小を、不等号を使って表しなさい。
(1) \( \sqrt{3},\ 3\) (2) \( \sqrt{0.3},\ 0.3\)

コメント