前回は,数直線上で線分の距離や内分点・外分点を考えました。ここでは,平面上での線分の距離や内分点・外分点やその他の重要な事柄を学習していきます。
座標平面上の2点間の距離
ここでは,座標平面上の2点\( A\left( x_{1},y_{2}\right) ,B\left( x_{2},y_{2}\right) \) 間の距離\(AB \)を求めていきます。
直線\(AB \)が座標軸に平行でないとき
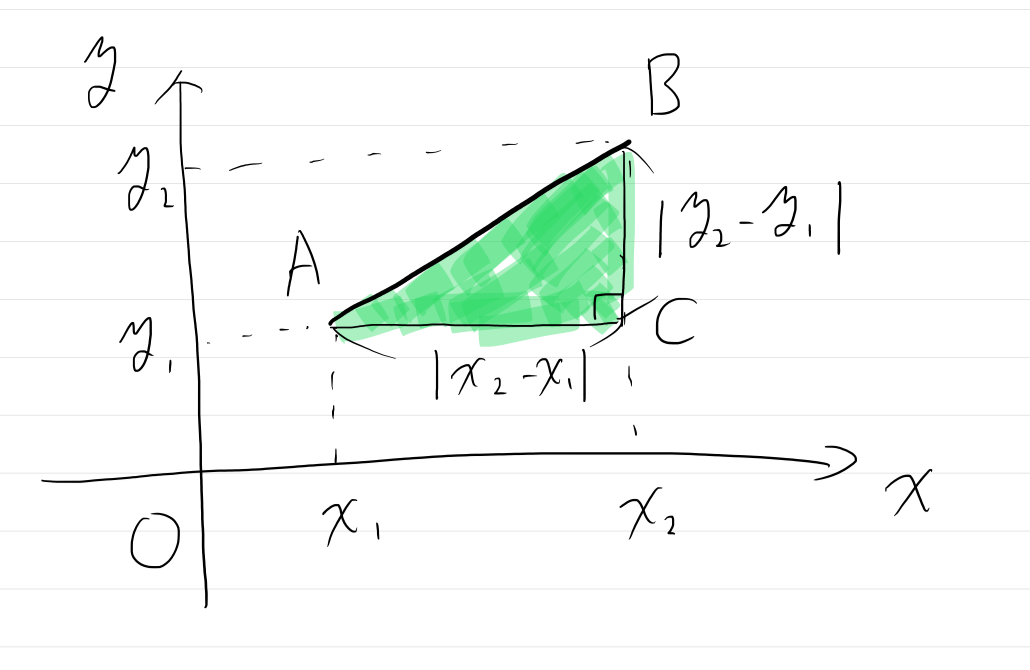
下の図の直角三角形\( ABC\)において
\begin{aligned}AC & =\left| x_{2}-x_{1}\right| ,\\
BC & =\left| y_{2}-y_{1}\right| \end{aligned}となる.

三平方の定理により,\(AB^{2}=AC^{2}+BC^{2} \) が成り立つので,
\begin{aligned}AB & =\sqrt{\left| x_{2}-x_{1}\right| ^{2}+\left| y_{2}-y_{1}\right| ^{2}}\\
&=\sqrt{\left( x_{2}-x_{1}\right) ^{2}+\left( y_{2}-y_{1}\right) ^{2}}\end{aligned}
この式は,直線\(AB \)が座標軸に平行なときにも成り立つ.
線分の内分点,外分点の座標
ここでは,座標平面上の2点\( A\left( x_{1},y_{2}\right) ,B\left( x_{2},y_{2}\right) \)を結ぶ線分を\(m:n \)に内分する点の座標を求めていきます
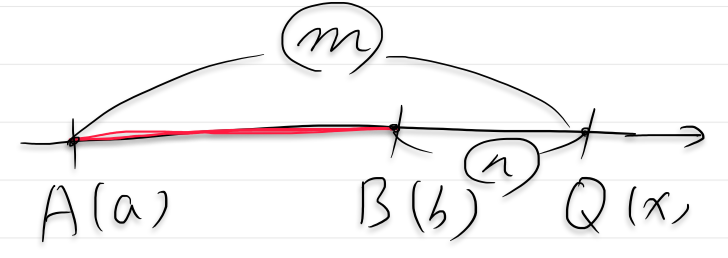
直線が\( x\)軸に垂直でないとき,\( A\),\( B\),\( P\)から\(x \)軸に,それぞれ垂線\( AA’\),\( BB’\),\( PP’\)を下ろすと,点\( P’\)は線分\(A’B’ \)を\(m:n \)に内分する.

よって,数直線上の内分点の公式より
\[x=\dfrac{nx_{1}+mx_{2}}{m+n}\cdots ①\]
直線\(AB \)が\( x\)軸に垂直であるときも,\( x=x_{1}=x_{2}\) で①が成立する.
\( P\)の\( y\)座標についても,同様に
\[ y=\dfrac{ny_{1}+my_{2}}{m+n} \]
また,外分点の座標についても,同様に考えて求めることができる.
重心
三角形の3本の中線は1点で交わり、その点は各中線を\(2:1 \)に内分します。この点を三角形の重心といいました。
ここでは,3点\(A\left( x_{1},y_{1}\right) ,B\left( x_{2},y_{2}\right) ,C\left( x_{3},y_{3}\right) \)を頂点とする\(\triangle ABC\)の重心\(G\left( x,y\right) \)の座標を求めていきます。
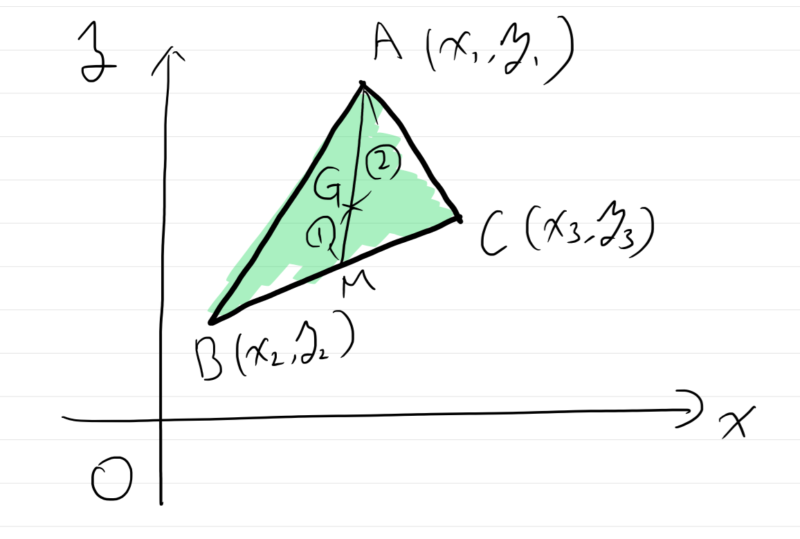
辺\( BC\)の中点\( M\)の座標は
\[\left( \dfrac{x_{2}+x_{3}}{2},\dfrac{y_{2}+y_{3}}{2}\right) \]
\( G\)は中線\(AM \)を\( 2:1\)に内分する点であるので,\begin{aligned}x & =\dfrac{1\cdot x_{1}+2\cdot \dfrac{x_{2}+x_{3}}{2}}{2+1}\\ &=\dfrac{x_{1}+x_{2}+x_{3}}{3}\end{aligned}同様にして,
\[y=\dfrac{y_{1}+z_{2}+z_{3}}{3}\]よって,重心\( G\)の座標は,次のようになる.
\[\left( \dfrac{x_{1}+x_{2}+x_{3}}{3},\dfrac{y_{1}+y_{2}+y_{3}}{3}\right) \]
点に関して対称な点
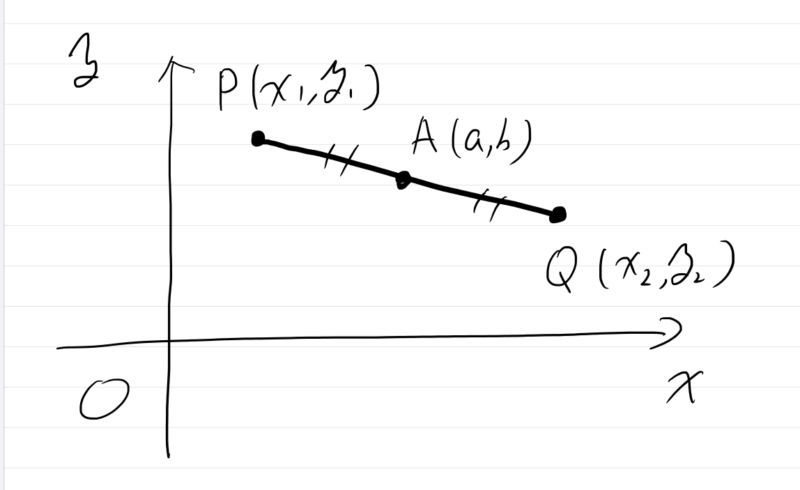
点\( A\left( a,b\right) \)に関して,2点\( P\left( x_{1},y_{1}\right) ,Q\left( x_{2},y_{2}\right) \)
が対称であるとき,\( A\)は線分\(PQ \)の中点であるから,次の等式が成立します.\[a=\dfrac{x_{1}+x_{2}}{2},\ \ b=\dfrac{y_{1}+y_{2}}{2}\]

コメント